旋翼无人机的两类主要算法

先说一个旋翼类无人机系统的算法主要有两类：姿态检测算法、姿态控制算法。

姿态控制、被控对象（即四旋翼无人机）、姿态检测三个部分构成一个闭环控制系统。被控对象的模型是由其物理系统决定，我们设计无人机的算法就是设计姿态控制算法、姿态检测算法。

1:姿态检测算法：姿态的三个自由度可以用欧拉角表示，也可以用四元数表示。姿态检测算法的作用就是将加速度计、陀螺仪等传感器的测量值解算成姿态，进而作为系统的反馈量。常用的姿态检测算法有卡尔曼滤波、互补滤波等。

2:姿态控制算法：控制飞行器姿态的三个自由度，以给定姿态与姿态检测算法得出的姿态偏差作为输入，被控对象模型的输入量作为输出（例如姿态增量），从而达到控制飞行器姿态的作用。最常用的就是PID控制及其各种PID扩展（分段、模糊等）、高端点的有自适应控制。当然，姿态控制算法里面又常用角速度、角度双闭环控制，所以常常有PD外环+PID内环等等。

无人机的稳定决定一切

造出一架合格的无人机并不需要花里胡哨的app，稳定决定一切。而稳定又是靠传感器决定的，传感器不准怎么办？当然是靠滤波算法。

加速度计、陀螺仪等传感器的数据，在现实中，是很“脏”的，也就是说被各种噪声污染得很厉害。要从大量噪声中过滤出真实的传感器数据，这就在姿态测算里涉及到滤波。

大疆的滤波算法就是一个非常核心的竞争力。因此无人机公司的核心产品的核心滤波算法，全公司也就只有那么一两个人知道，他们平时坐在研发的一个小角落里，深藏不露。

卡尔曼滤波

网上广为流传着几篇关于卡尔曼滤波的科普文章，但是都夹杂着一堆复杂的公式，不知道你看后是一种什么样的感觉，我看时，看的我如坠云雾里。我希望能看到一篇没有复杂数学公式的文章，却一直没找到。

于是我想写一篇，讲讲自己对卡尔曼滤波的浅显理解。

我觉得卡尔曼滤波算法本质上是一个递推反馈算法。它分两部分：时间更新方程和测量状态更新方程。其中，前者负责递推，后者负责反馈（将先验估计和新的测量变量结合，以构造改进后的后验估计）。

时间更新方程可视为预估方程，测量更新方程可视为校正方程。

这个是预估方程：

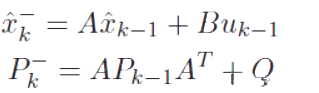
x表示状态变量；左上角带“—”的量表示先验；“ ^ ”表示估计。

“先验”与“后验”是相对的俩概念，“先验”的意思就是仅仅用之前的状态来估计出来的；而“后验”是在我们进行了测量，知道了测量变量 z 之后的。也就是说，“先验”与“后验”的区别就是有没有进行测量。

预估方程可以这么理解：因为卡尔曼滤波算法的前提条件是：系统是线性的。所以即使不用测量，我们也可以根据“线性”这个特征得到一个先验状态值。

这个是校正方程：

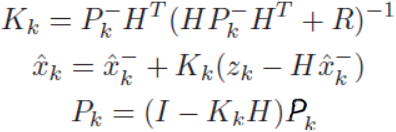
中间的那个式子做一下整理就容易理解了：把先验状态变量提出来放到一块儿。

那这个校正方程就可以这么理解了：有了测量值之后，我们便有了两个可用的量了，即测量值z和先验状态值，那我们就根据这两个量之前的表现来各自给他们分配一个权重（之前表现越好的量，其权重就越高），这个权重就是卡尔曼增益。那么什么是表现好表现不好呢，表现好意思就是测量结果稳定，方差很小，表现不好就是估计值或观测值不稳定、方差很大。

最后再付一个图基本就差不多了。

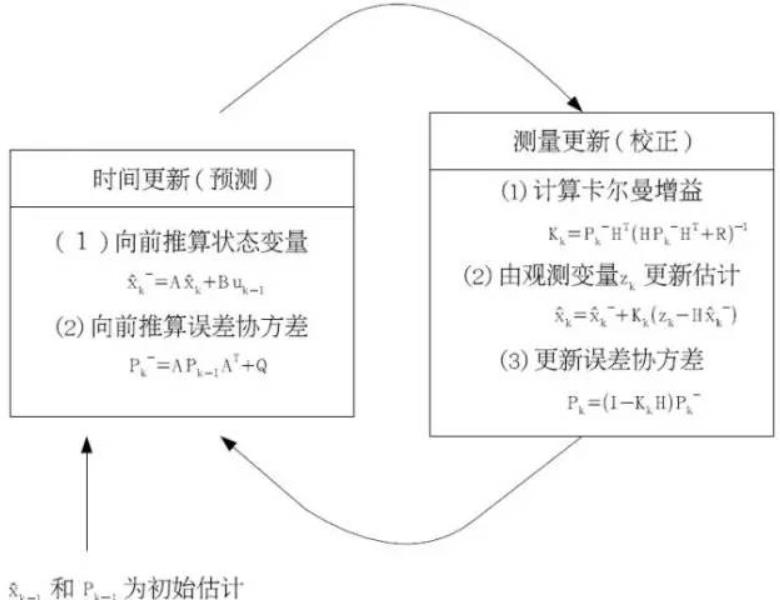
讲到这儿我觉得基本就可以了，最起码在以后生疏之后再看一遍这篇文章，基本就能回想起卡尔曼。

要不最后再说说卡尔曼滤波算法能干嘛吧，我觉得基本上的应用有两个，一个是测量，一个是预测。

一架飞机在天上飞，我们想知道这架飞行在任一时刻所处的位置、速度等状态参数，那我们就得用测量装置进行测量，这样问题就来了。因为测量装置存在随机干扰，所以它测得的结果中就会夹杂着大量随机干扰，这时测量装置返回来的状态参数是不靠谱的。

那怎么办呢？这就用到了卡尔曼滤波算法，因为卡尔曼滤波的核心是“预测+校正”，所以在测量上，我们用到的就是校正出来后验状态变量。

卡尔曼在博士毕业的时候拿着卡尔曼滤波算法作为他毕业论文的主题，唉……差距啊，他这么吊，也不知道他爸妈知不知道。

看到这儿你可能还有点蒙，我们再来通俗的举例子说明。

假设你有两个传感器，测的是同一个信号。可是它们每次的读数都不太一样，怎么办？

取平均。

再假设你知道其中贵的那个传感器应该准一些，便宜的那个应该差一些。那有比取平均更好的办法吗？

加权平均。

怎么加权？假设两个传感器的误差都符合正态分布，假设你知道这两个正态分布的方差，用这两个方差值，（此处省略若干数学公式），你可以得到一个“最优”的权重。

接下来，重点来了：假设你只有一个传感器，但是你还有一个数学模型。模型可以帮你算出一个值，但也不是那么准。怎么办？

把模型算出来的值，和传感器测出的值，（就像两个传感器那样），取加权平均。

OK，最后一点说明：你的模型其实只是一个步长的，也就是说，知道x(k)，我可以求x(k+1)。问题是x(k)是多少呢？

答案：x(k)就是你上一步卡尔曼滤波得到的、所谓加权平均之后的那个、对x在k时刻的最佳估计值。

于是迭代也有了。

这就是卡尔曼滤波。

知道一点卡尔曼滤波比较好

作为一个无人机从业者，或许你不是搞算法的、或许你也不是搞飞控的，你可能只是做结构的、业务的，这都没有关系。但要作为一个资深的无人机从业者，对于无人机的来龙去脉，技术等方面的全面了解，笔者认为是有必要的。

其实，"算法"到最后最是数学问题,整理再多,不会用全白搭！就是网上很多的源码直接抄，用在你的代码里，你不明白原理，还是白搭！